Spatial-Partitioning-Quadtree

Spatial ordering optimization: Quadtree

Project maintained by CarlosUPC Hosted on GitHub Pages — Theme by mattgraham

I am Carlos Peña Hernando, student of the Bachelor’s Degree in Video Games by UPC at CITM. This content is generated as a game development research for learning purposes at my free time.

Search Conception

First of all, in order to talk about the topic we are here, It is very important to start with a brief introduction about the concept of “search” in the computational world. The concept of search comes from search engine/ tool code which, as the name implies, searches for certain types of elements in an area of the space.

This search stick to a rule or rules, such as “search for all elements found at a radius X of this point” , “Search for the element closest to this point”, … Starting from these rules of searching, there are different ways to sort the space to perform the search.

Application in Videogames

Search engine is a fundamental tool which at the time was used and nowadays is still used to simulate so many features that have archieved very positive results in videogames.

For example, in a game like Age of Empires, if you tell a villager to “cut down trees to get wood,” the villager from the position where he is will look for the nearest tree and when he finds it with the search engine, a pathfinding algorithm will be performed to go to the tree. Once it is finished, if the order has not been revoked, you can search for a nearby tree on a radius with the search engine and retrace the pathfinding to this one, if it does not find any, you can tell it to look for the nearest building and shelter, again with the search engine, but instead of looking for tree entities, look for building entities.

Another example may be tower defense games. There are enemies that are advancing in a route, and the towers of defense look for with the engine, enemies that are in range of attack, if so, they attack. Once you have eliminated the target, look for another enemy in range, if there is one, attack, if not, keep doing checks on each frame or every X frames in the search for another enemy.

Issue’s Point

Applied to video games, if we want to find a type of entity of the world in a limited area/range, such as to check collisions, render tile maps, render 3D objects, etc. The first solutions that comes to our mind will usually be an exhaustive search, also called brute force search.

As its name says, this algorithms are generally problem-solving, but they scale with the size of candidates they have to check., working OK with a low amount of them but making our game unplayable if the amount is high.

For example, in order to check the collisions of the particles of the system in the image, if we used a brute force algorithm, we would check each particle colliding with the others, no matter their position.

If we are working with a low amount of particles like in this image, we would iterate 72 (8x8) times each frame. But let’s say we are working with 100 particles, we would need 10.000 (100x100) iterations each frame.

In case that we have 1000 collision, we are talking about 1000 * 1000 = 1.000.000 checks and so on. Thus, we can see that the check collisions have a cost of elements^2.

So, now imagine how many iterations we would need in a scene like this one:

A really big headache, don’t you think?

That’s where spatial partitioning algorithms appears to save this issue :)

Space partitioning

In order to avoid iterations that are not needed (colliders too far from each other, tiles / polygons out of the screen), we can divide the space into different subsets.

That process is called space partition. There are a lot of ways to divide the space, and depending on our needs we will choose one or another.

BSP (Binary Search Partition): First used in Doom, to optimize the process and ordering by distance. It cuts the space in hyperplanes and keep branching top/bottom of the plane.

QUADTREE: divides the space into 4 subsets, each of them might be divided into 4 subsets, etc.

OCTREE: similar to the quadtrees, but used in 3D instead of 2D. Each node will have 8 children instead of 4.

K-D TREE: the space is divided into 2 subspaces, which might not be equal. The “partition lines” are always perpendicular to the coordinates axis.

AABB TREE: Creates subspaces for each group of elements we need to check. Mostly used in dynamic entities like collisions.

As you cans see in the images above, these data structures translate the space into nodes, which have more subnodes. This structure can be represented in tree diagrams, that’s why they are called trees.

This are just a few ways to part the space explained vrey superficially. There are a lot more of them, and honestly, we could spend an entire semester talking about different space partition algorithms, but in this article I’m going to focus on Quadtrees.

QUADTREE

As a approached method to work with, Quadtree is the space partitioning algorithm i choose to develop an optimized collision system you can find in the demo application i made in my repository.

As I said before, quadtrees are a data structure that divide the space into 4 sub regions. Each node will have four children, which will have four children each, etc.

Even though I’m going to use them for a “videogame” aproach, they can be used in a lot of fields, such as image compression.

Quadtree’s Approaches

The main cases where Quadtree comes to are the following ones:

Camera Culling: When we are playing a video game, we don’t need to render all the map, in fact, we must not, because it’s a waste of time. As I said at the beggining, if the map isn’t really big, it’s not a big deal, but most of the cases it won’t be like that, and especially in tiled maps we need to optimize the render process. Let me put into situation. Let’s say I’m developing an RTS with a map of 256x256 tiles. That’s a total amount of 65.536 tiles, from which only 500 will appear in the screen, more or less. What we want to do is to only go across those tiles that appear int the screen, instead of going across all of them and only printing those that are in the screen.
Collision Checking: This case is more difficult than camera culling because the set of tiles is static but entities and particles are dynamic. In this case we need to create a dynamic QuadTree that always changes along with entities.

This it’s slower than the quadtree mentioned before but it’s faster than the exhaustive method.

Region-Point Quadtree

There are different types of quadtrees, but I will focus on the Region-Point Quadtrees, which are the most common and I think will be the most useful in a 2D game.

This quadtree divide the total space into four equal regions, which will be divided into four equal regions and so on until we reach the nodes that are at the bottom of the tree.

Quadtree subdivisions:

Quadtree’s Goal

This type of structure is more related to recursive functions system since Quadtree starts working in its first quad level (also called as root) and from that root, recursively it calls its subnodes until we reach the last level depth / bottom level of the Quadtree.

Once Quadtree is explained, we know how quadtrees work at a concept view, but how can quadtrees fit in our game? in other words, what’s the goal of quadtree in our game?

Let’s put forward this question with the following image:

In the first frame we see how the space is not divided, therefore, we check collisions between all the particles (brute force). And in a system for only 20 particles, we need 400 iterations for each frame. It’s important to know that the checks we make increase exponentially as we add more particles: with 10 particles we need 100 iterations, with 20 particles, 400 iterations, with 30 particles, 900 iterations, and so on.
In the second frame the space is divided into four subspaces, and each particle only checks its collision with the other particles in its own subspace. As you can see, it reduces the number of iterations a lot.
And in the third frame, we divide all the previous subspaces that had more than 3 particles. As you can see, there are some subspaces which only have one particle, so we won’t even need to check their collision.

Only by dividing the space twice, improved the performance of our system in a 1279%, by going from 400 iterations each frame to 29 iterations. Incredible, right?

This goal, is indeed the main ambition from myself to archieve an optimized Collision checking using a Region-Point Quadtree

Quadtree code structure

Allright! time to dive to the research and let’s talk about the code structure of my Quadtree approach.

At the beginning of my research, i documented myself about everything related to the search and partition algorithms obviously focusing on the quadtree. After an exhaustive investigation, i perform some small experiments throught web and video tutorials programming a quadtree in javascript and visualizing the result in p5. You can see the result here!

To understand even more deeply the use of this partition algorithm, i developed an optimized collision system with Quadtree in javascript and p5, also with the help of tutorials. You can check the demo here!

At this point, i got on and developed a Quadtree code structure according to my thoughts and learning experiments. The following image below, shows you the core Quadtree structure from my code.

And the next one, shows you the structuree of each node / bucket from Quadtree which i so-called “QuadNode”

Maybe we could find this elements in any quadtree, but this one has the peculiarity that it starts with a root from the quadtree, which recursively increases the number of nodes. I found this option very attractive and it fit very well with the algorithm idea of a quadtree. That is why I have separated the code into two parts: Quadtree and Quadnode.

Some functions might change, but the overall purpose will be the same. Obviously, we will need more methods and variables depending on what we use our quadtrees for, but this would be a nice parent class.

The fact that they are templated containers does not mean that they have to be, this is how I made it, but as I said at the beginning, you can find your own way of coding them.

Basically, all we need is a rectangle that tells us the area the node is occupying (boundary).

Variables like BucketSize and Depth represent the capacity of elements within a node and its depth level the node is in the tree which when it becomes to the last level of depth, this node turn out a leaf node and won’t be subdivided.

Booleans like leaf and divided just serve as states to identify if node is at the bottom of the tree or is divided.

And obviously, an array with all the subnodes and an array with the elements that node will store.

Quadtree Functionalities:

When it comes to the methods, the most important one is the Split(), which will divide the node into 4 subnodes.

Another important one is Insert() method, which add all the elements to the element array from the respective node

To retrieve all the elements within a respective node to check, for example collisions, we will use Query()

Then we have the Draw() which, guess what, is going to draw the quadtree rects.

TODO’s and Solutions

TODO0: XML Configuration

Explication:

Pretty easy one! Fill the following variables from config.xml file provided in the project using pugi API code. You can edit and configure the values anytime you want to test Quadtree performance.

Solution:

bool j1Collision::Awake(pugi::xml_node& config)
{
	qtree_rect.x = config.child("quadtree").attribute("qt_x").as_float();
	qtree_rect.y = config.child("quadtree").attribute("qt_y").as_float();
	qtree_rect.w = config.child("quadtree").attribute("qt_width").as_float();
	qtree_rect.h = config.child("quadtree").attribute("qt_height").as_float();

	capacity = config.child("quadtree").attribute("capacity").as_int();
	depth = config.child("quadtree").attribute("depth").as_int();

	return true;
}

TODO1: Allocate Quadtree memory

Explication:

You can’t fail this one! Just allocate quadtree memory using qtree pointer declared already and fill the parameter fields using the values you previously defined in TODO0.

Solution:

bool j1Collision::Start()
{
	qtree = new Quadtree<Collider>({qtree_rect.x, qtree_rect.y, qtree_rect.w, qtree_rect.h}, capacity, depth);
	return true;
}

TODO2: Split nodes

Explication:

Until now its being too easy, now its time to complicate the stuff. Be ready to subdivide the root node allocating memory into its child nodes. Remember to calculate well the new boundary coordinates and increase the level of depth by 1!

Solution:

template<class T>
 void QuadNode<T>::Split()
{

	nodes[NORTHWEST] = new QuadNode<T>({ boundary.x,boundary.y, boundary.w / 2, boundary.h / 2 }, this->BucketSize, this->depth + 1, this->callback);

	nodes[NORTHEAST] = new QuadNode<T>({ boundary.x + boundary.w / 2,boundary.y,boundary.w / 2, boundary.h / 2 }, this->BucketSize, this->depth + 1, this->callback);

	nodes[SOUTHWEST] = new QuadNode<T>({ boundary.x,boundary.y + boundary.h / 2 , boundary.w / 2, boundary.h / 2 }, this->BucketSize, this->depth + 1, this->callback);

	nodes[SOUTHEAST] = new QuadNode<T>({ boundary.x + boundary.w / 2 ,boundary.y + boundary.h / 2, boundary.w / 2,  boundary.h / 2 }, this->BucketSize, this->depth + 1, this->callback);

	this->divided = true;

}

TODO3: Insert()

Explication:

First of all, we need to check if data is contained in respective bucket (you can use Contains() function). After get it,There are different ways of doing it but i recommend to push the data parameter into element array from each node/bucket if the capacity is not overloaded.

If so, Use the function you made it to subdivide that node and pass all its elements stored into the new child nodes distributing them correctly. Remember to make it recursively using Insert() function with the children of respective bucket when we are not in the leaf node.

Solution:

template<typename T>
 inline bool QuadNode<T>::Insert(T* data)
 {

	 if (!this->Contains(*data))
		 return false;


	 if (this->leaf) // LEAF NODE
	 {
		 if (this->elements.size() < this->callback->GetMaxBucketSize())
		 {
			 this->elements.push_back(data);
			 return true;
		 }

		 else if (this->depth < this->callback->GetMaxDepth())
		 {
			 this->leaf = false;

			 if (!this->divided)
				 this->Split();


			 for (int i = 0; i < 4; ++i)
				 this->nodes[i]->Insert(data);
					

			typename std::list<T>::iterator it;

			for (std::list<T*>::iterator it = elements.begin(); it != elements.end(); it++)
			{

				for (int j = 0; j < 4; ++j)
					this->nodes[j]->Insert(*it);	

			}

			this->elements.clear();
		 }
	 }
	 else // STEM NODE
	 {

		 for (int i = 0; i < 4; ++i)
			 this->nodes[i]->Insert(data);
				
	 }




 }

 
 double j1Collision::QuadTreeChecking()
{
	double quadTreeTime;
	quadTreeTimer.Start();

	
	qtree->CleanUp();

	for (std::list<Collider*>::iterator it = colliders.begin(); it != colliders.end(); it++) 
		qtree->Insert(*it);

		
	quadTreeTime = quadTreeTimer.ReadMs();
	return quadTreeTime;
}

TODO4: Query()

Explication:

Similar TODO as the last one, we need to check if data is contained in respective bucket (you can use Contains() function) and push all the elements you find into found std::list if we are at the bottom level. If not, make it recursively to use Query() function with the children of respective bucket.

Solution:

template<class T>
 inline void QuadNode<T>::Query(std::list<T*>& found, T* data)
 {

	 if (!this->Contains(*data))
		 return;

	 if (this->leaf) // LEAF NODE
	 {
		 typename std::list<T>::iterator it;

		 for (std::list<T*>::iterator it = elements.begin(); it != elements.end(); it++)
		 {
			 if(data != *it)
				found.push_back(*it);
		 }

	 }
	 else // STEM NODE
	 {

		 for (int i = 0; i < 4; ++i)
			 this->nodes[i]->Query(found, data);

	 }


 }
 

TODO5: Collision Checking

Explication:

Okey, at this point we are almost done! Just make the same functionality you can see in BruteForceChecking() function but changing the logic of second loop a bit. We need to call the Query() function to retrieve all of the elements from each bucket into an array (you can use “found” std::list from Quadtree container). Once you get it, iterate it in second loop to check collisions as BruteForce funcion does. Remember to clean the array with retrieved elements because we are doing this every frame!

Solution:

 
double j1Collision::QuadTreeChecking()
{
	double quadTreeTime;
	quadTreeTimer.Start();

	
	qtree->CleanUp();

	for (std::list<Collider*>::iterator it = colliders.begin(); it != colliders.end(); it++) 
		qtree->Insert(*it);

		

	quadTreeChecks = 0;

	for (std::list<Collider*>::iterator it = colliders.begin(); it != colliders.end(); it++)
	{
		qtree->found.clear();
		qtree->Query(qtree->found, *it);

		if (qtree->found.size() > 0)
		{
			LOG("Colliders near found: %i", qtree->found.size());

			for (std::list<Collider*>::iterator it2 = qtree->found.begin(); it2 != qtree->found.end(); it2++) 
			{
				if ((*it)->CheckCollision((*it2)->rect)) {

					if (matrix[(*it)->type][(*it2)->type] && (*it)->callback)
						(*it)->callback->OnCollision((*it), (*it2));

					if (matrix[(*it2)->type][(*it)->type] && (*it2)->callback)
						(*it2)->callback->OnCollision((*it2), (*it));

				}
				quadTreeChecks++;
				
				App->render->DrawQuad((*it2)->rect, 0, 255, 0, 255, false);
				App->render->DrawLine((*it)->rect.x + (*it)->rect.w / 2, (*it)->rect.y + (*it)->rect.h / 2, (*it2)->rect.x + (*it2)->rect.w / 2, (*it2)->rect.y + (*it2)->rect.h / 2, 0, 255, 255, 255);
			}

		}

	}

	quadTreeTime = quadTreeTimer.ReadMs();
	return quadTreeTime;
}

TODO5: Draw() & CleanUp()

Explication:

Call Quadtree Draw function in the update. You can use the boolean “debugQT” to make a condition that when this boolean becomes true, Draw is called. To wrap up, remeber to call Quadtree CleanUp function and delete qtree pointer to free its memory.

Solution:

  if(debugQT)
	qtree->Draw();

    qtree->CleanUp();
    delete qtree;
    qtree = nullptr;

FINAL RESULTS

Time to see how our application is doing. Let’s see how Quadtree’s optimization performs upon the application against a recursive search as Brute Force. to get an obvious conclusions of this comparison, we will work with 1000 entities and see what are the performance result using both methods.

Brute Force Performance

Instantiating and drawing 1000 entities using Brute Force we get this:

In the gif above, you can perceive a certain lag because of low framerate the game goes produced for the huge number of iterations that have to be done to check collisions at 1000 entities. Remember that when Brute Force comes in, its number of iterations will be 1000x1000 if we take in account that we are working with this number of entities.

Debug Info:

As debug result, we obtain a game which each frame is performed with an average of 198.94 ms. A truly big game issue for us if we need to work with 1000 entities!

Quadtree Performance

Instantiating and drawing 1000 entities using Quatree we get this:

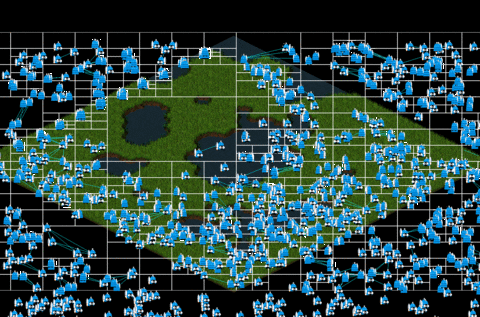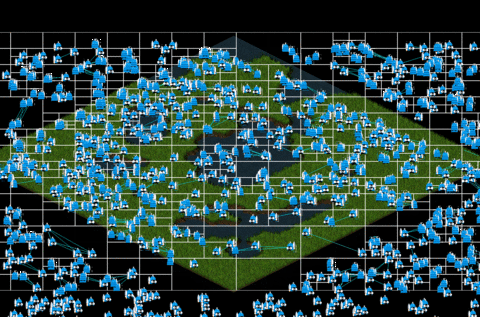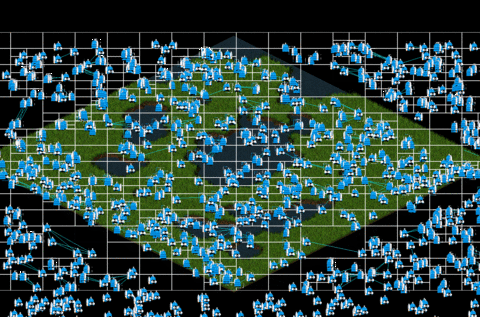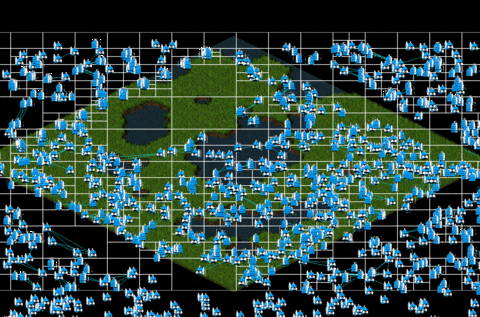
In the gif above, you can perceive that there is no lag as the previous fig has. That is possible since with quadtree method, we don’t need to iterate all the elements instantiated, just the ones which are contained in each node, so the iterations decrease considerately from 1000x1000 iterations to only 1530 iterations! The optimizations seems like work perfectly!

Debug Info:

As debug result, we obtain a game which each frame is performed with an average of 38.9 ms. An incredible improvement, don’t you think?

As you can see here, it’s really important to optimize the drawing methods of our games. We’ve gone from iterating 1000x1000 each frame, to iterating only those that are on each bucket, which are 1530 iterations. This value might change a bit depending on the position of our entities if they are moving as the demo does, but it wouldn’t make a big difference.

And how does this affect the performance of our game? Well, let’s see:

The numbers at the left, show the time spent drawing the entities with quadtrees, and the ones at the right show the time spent using brute force. From spending more than 200 ms each frame to draw the entities, we now spend 0.040 seconds. So we improved the performance of our game in a roughly 25%, not bad at all!